Leeftijd
Hoe oud is ons heelal nu? Via de Big Bang-theorie krijgen we hierop wel een redelijk antwoord, maar ook waarnemingen die niets met deze theorie te maken hebben, wijzen erop dat het heelal wel degelijk een begin gehad heeft, en geven ons een onafhankelijke schatting van haar leeftijd.
We halen hier enkele indicaties en metingen aan:
- De paradox van Olbers
- De abundantie van Uranium-isotopen
- De leeftijd van de oudste sterren
- De uitdijing van het heelal
Het feit dat de resultaten uit bovenstaande technieken mekaar niet tegenspreken, en zelfs waarden uitkomen die sterk in mekaars buurt liggen, verhoogt de geloofwaardigheid van de Big Bang-theorie.
De paradox van Olbers
 Stel dat het heelal statisch en oneindig is: dat het gelijkmatig gevuld is met sterren/sterrenstelsels, en dat er altijd sterren/sterrenstelsels zijn geweest. Hoe helder moet de nachtelijke hemel dan zijn?
Stel dat het heelal statisch en oneindig is: dat het gelijkmatig gevuld is met sterren/sterrenstelsels, en dat er altijd sterren/sterrenstelsels zijn geweest. Hoe helder moet de nachtelijke hemel dan zijn?
De lichtintensiteit van een lichtbron neemt af met het kwadraat van de afstand: als we 3 keer verder gaan staan van een lichtbron, krijgen we er 9 keer minder licht van. Als we het volume van een bolvormige schil, met gegeven dikte, om de aarde gaan berekenen, dan zien we dat het toeneemt met het kwadraat van de afstand. Een schil van 1 lichtjaar dikte op een afstand van 3000 lichtjaar, heeft een volume dat 9 keer groter is dan een schil van 1 lichtjaar op 1000 lichtjaar.
Als we nu, zoals eerder gesteld, veronderstellen dat sterren/sterrenstelsels homogeen verdeeld zijn (overal zelfde aantal per volume-eenheid), betekent dat dus dat een schil op 3000 lichtjaar 9 keer meer sterren zal bevatten dan eentje op 1000 lichtjaar. Daardoor zal die schil ook 9 keer meer licht uitsturen, maar door de afstand zien we die ook 9 keer zwakker. Alle schillen zullen dus, onafhankelijk van de afstand waarop ze staan, vanop aarde even helder lijken.
In een oneindig heelal, waar zelfs het licht van oneindig verre schillen ons heeft kunnen bereiken, moet de nachthemel door de optelling van al die schillen dus oneindig helder zijn! Zelfs als we rekening houden met het feit dat een ster een andere kan bedekken, moeten we tot de vaststelling komen dat elk punt aan de hemel dan even helder zou moeten zijn als de zonneschijf: in elke richting stoten we namelijk rechtstreeks op een steroppervlak ...
We weten dat dat niet zo is: de nachtelijke hemel is wel degelijk donker. Kunnen donkere stofwolken, waarvan we weten dat ze veelvuldig voorkomen in het heelal, misschien niet gewoon ons zicht belemmeren? Dat kan, maar dit stof zou door de absorptie van het licht opgewarmd worden, tot het uiteindelijk zou beginnen gloeien en zelf licht beginnen uitstralen, wat tot hetzelfde resultaat zou leiden.
De oplossing van het paradox van Olbers ligt in het feit dat het heelal een eindige leeftijd heeft, en dus op een zeker moment is ontstaan. Al is het heelal oneindig groot en volledig gevuld met sterren, het licht van verre schillen heeft ons nog niet kunnen bereiken, omdat het nog maar een eindige tijd naar ons onderweg is.
Het is waar dat een groot deel van het verre licht wordt geabsorbeerd door interstellair stof, maar dit gebeurt nog niet lang genoeg en niet met voldoende lichtintensiteit om dat stof significant op te warmen. Bovendien zorgt de kosmische roodverschuiving ten gevolge van de uitdijing van het heelal voor een verlies aan energie van de verste schillen. De kosmische achtergrondstraling (licht van een bron van 3000K op een schil op 13.8 miljard lichtjaar) is hier een mooi voorbeeld van.
De abundantie van Uranium-isotopen
Uranium is een radioactief element. Dat wil zeggen dat het de neiging heeft om na verloop van tijd spontaan over te gaan in een ander element, in dit geval Thorium. Deze spontane metamorfose noemen we het radioactief verval.
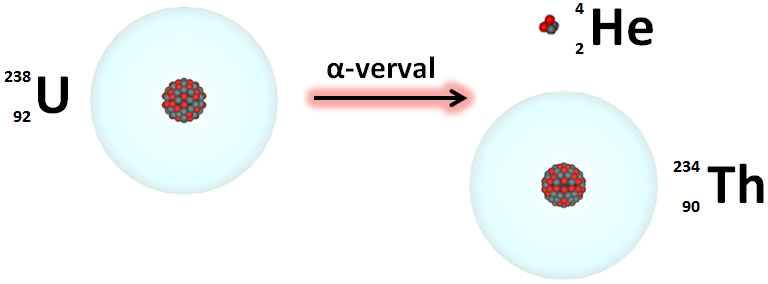
Er bestaan verschillende soorten (isotopen) Uranium, met elk een verschillend aantal neutronen in de atoomkern. De halfwaardetijd, de typische tijd die verloopt alvorens de helft van een portie Uranium radioactief is vervallen, is verschillend naargelang de isotoop.
| Isotoop | Halfwaardetijd | Vervalt naar |
| Uranium | 234 244 500 jaar | Thorium 230 |
| Uranium | 235 703.8 miljoen jaar | Thorium 231 |
| Uranium | 238 4.468 miljard jaar | Thorium 234 |
Uranium-kernen worden gevormd wanneer sterren, aan het einde van hun leven, ontploffen in een supernova-explosie. We kunnen berekenen dat bij die gebeurtenis ongeveer 1.65 keer meer U235 dan U238 ontstaat. Nu zien we echter dat er in het interstellaire gas in ons melkwegstelsel 139 keer meer U238 dan U235 is. Hieruit kan men besluiten dat het interstellaire gas in ons melkwegstelsel zeker niet jonger is dan 6.6 miljard jaar. Daarbij moet natuurlijk nog de tijd gerekend worden, nodig om het melkwegstelsel te doen ontstaan (ca. 1 miljard jaar), en deze nodig om een ster tot een supernova te laten evolueren (minimum ca. 100 miljoen jaar). Bovendien is de schatting een benedengrens, want telkens een supernova ontploft, wordt nieuw Uranium aangemaakt en in het interstellaire gas gestort.
De leeftijd van de oudste sterren
In plaats van naar het gas in de ruimte te kijken, kunnen we ook naar sterren kijken. Die zijn eenvoudiger te onderzoeken, want daar kunnen we de geschiedenis veel nauwkeuriger van narekenen. De oudste sterren vinden we in bolhopen: bolvormige groeperingen van enkele tienduizenden à honderdduizenden sterren, die rond ons melkwegstelsel draaien. Ze zijn samen met ons melkwegstelsel ontstaan, wellicht zo'n miljard jaar na de Big Bang. Als we de samenstelling van deze sterren bekijken, zien we inderdaad dat zij bijna uitsluitend bestaan uit waterstof en helium, en dus niet vervuild zijn door zwaardere elementen (metalen) in supernova's. De sterren die bhoren tot de melkwegschijf zijn de ongste. Binnen de melkweg worden voortdurend nieuwe sterren gevormd, het zijn dan ook de jongste: populatie I. Negentig procent van de sterren waaruit de Bolhopen bestaan die de melkwegschijf omgeven, zijn veel ouder: populatie II. Zo nu en dan, heel zeldzaam vindt men nog sterren die uitsluitend uit waterstof en helium bestaan. Het gaat hier om de allereerste sterren die gevormd zijn, 200 miljoen jaar na de Oerknal: populatie III.

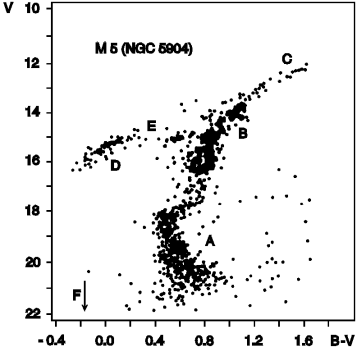
De sterren van bolhoop M5 in een Hertzsprung-Russell diagram, via hetwelke de sterevolutie onderzocht kan worden.
De verschillende letters komen overeen met sterren in verschillende levensfasen.
Hoe zwaarder een ster, hoe helderder ze is, maar ook hoe korter ze leeft. In een bolhoop kunnen we er veilig van uitgaan dat alle sterren tegelijk zijn ontstaan. Door hun helderheid en kleur nauwkeurig te bepalen, kan men nu onderzoeken in welke levensfase elke ster van de bolhoop zich exact bevindt. Uit het aantal sterren dat de hoofdreeks verlaten heeft, en een tak vormen rechts naar bovenin het diagram, kan de ouderdom van de bolhoop worden afgeleid.
Tot 1997 dacht men dat de oudste sterren die men waarnam zo'n 18 miljard jaar oud waren, wat dus ouder is dan het heelal zelf! Dit mysterie werd opgelost toen de Hipparcos-satelliet ontdekte dat een aantal sterren, die als mijlpaal gebruikt worden voor het meten van afstanden in het heelal, dichterbij staan dan gedacht. Daarvoor had men dus steeds de absolute helderheid, en dus de massa, van sterren in de bolhopen overschat.
Nu schatten we dat de oudste sterren zo'n 10 à 13 miljard jaar oud zijn. Tel daar nog een miljard jaar bij voor het ontstaan van de melkwegstelsels en bijhorende bolhopen, en we komen op een leeftijd van 11 à 14 miljard jaar voor het heelal.
De uitdijing van het heelal
Natuurlijk geeft de Big Bang-theorie zelf ook een schatting voor de leeftijd van het heelal, via de uitdijingssnelheid (constante van Hubble). Als we weten hoe het heelal uitdijt, en hoe de uitdijingssnelheid evolueert, kan de leeftijd van het heelal teruggerekend worden. Volgens deze methode ligt de leeftijd van het heelal ergens tussen 8 en 13 miljard jaar. Deze schatting is wel nog afhankelijk van de kromming van het heelal.
Verwante links
- The age of the universe: Meer gedetailleerde voorbeelden, en enkele andere technieken voor leeftijdsbepaling van het heelal.
- Olber's Paradox: Een iets wiskundigere benadering van de oplossing van de paradox van Olbers.

