Planeetbanen
Planeten draaien om de zon. In dit deel bekijken we volgens welke fysische wetten dit gebeurt, en hoe banen beschreven worden.
Wetten van Kepler
Door gebruik te maken van nauwkeurige blote-oog-waarnemingen van zijn voorganger Tycho Brahe, slaagde Johannes Kepler er in het begin van de 17de eeuw in de beweging van de planeten omheen de zon vast te leggen in drie wetten, die vervolgens naar hem genoemd werden. Later werden deze wetten bewezen door middel van de gravitatiewet van Isaac Newton.
Met deze gravitatiewet in ons achterhoofd, formuleren we de wetten van Kepler iets algemener of iets fijner dan Kepler dat gedaan heeft.
Eerste wet
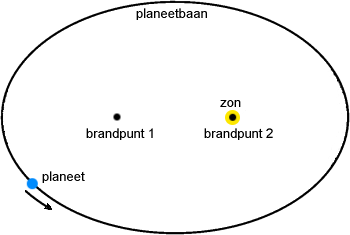
Een hemellichaam in de buurt van de zon beschrijft een kegelsnede (cirkel, ellips, parabool of hyperbool) met de zon in een brandpunt.
Wanneer het gaat om hemellichamen van het zonnestelsel, d.w.z. hemellichamen die een gesloten baan om de zon beschrijven, kan deze kegelsnede alleen maar een ellips zijn (of een cirkel), en bekomen we de traditionele formulering van de eerste wet van Kepler.
Een hemellichaam dat niet tot ons zonnestelsel behoort en dit toevallig doorklieft, zal in de buurt van de zon een segment van een hyperbooltak beschrijven. Hetzelfde geldt voor hemellichamen van ons zonnestelsel (in de praktijk kometen) die door één van de reuzenplaneten (meestal Jupiter) uit het zonnestelsel geslingerd worden.
De parabool is een overgangsfiguur tussen de ellips en de hyperbool. Omwille daarvan komen parabolische banen in de natuur eigenlijk niet voor. Vele kometen beschrijven echter dermate langgerekte ellipsvormige banen dat ze in de buurt van de zon nauwelijks van parabolen te onderscheiden vallen. Indien een dergelijke komeet ontdekt wordt, berekent met daarom met behulp van de eerste waarnemingsgegevens een parabolische baan om efemeriden voor die komeet te kunnen opstellen, en gaat men pas later een meer nauwkeurige elliptische baan bereken, als er voldoende waarnemingsgegevens beschikbaar zijn.
Tweede wet
De voerstraal van de zon naar een hemellichaam in een baan om de zon beschrijft perken waarvan de oppervlakte rechtevenredig is met de hiervoor benodigde tijd.
Oftewel:
In gelijke tijden doorloopt de lijn die de planeet met de zon verbindt, oppervlakten ("perken") van gelijke grootte.
Uit onderstaande figuur blijkt dat bijvoorbeeld een planeet beduidend sneller beweegt in de buurt van haar perihelium (dichtste nadering tot de zon) dan in de buurt van haar aphelium (punt van verste verwijdering tot de zon). De tweede wet van Kepler wordt ook de perkenwet genoemd.

Derde wet
De derde macht van de halve grote as van een hemellichaam in een ellipsbaan om de zon is rechtevenredig met het kwadraat van zijn omloopstijd.
Een hemellichaam dat vier keer zo ver van de zon staat als de aarde heeft dus achtmaal meer tijd nodig om één omloop te voltooien, wat dubbel zo veel is dan we zouden verwachten op basis van de omtrek van te doorlopen baan. De absolute snelheid van een hemellichaam in een baan om de zon neemt dus af met de afstand tot de zon!
De derde wet van Kepler kan worden gebruikt om de relatieve afmetingen van het zonnestelsel in kaart te brengen: door de omloopstijd van een hemellichaam te meten, kennen we zijn afstand tot de zon in astronomische eenheid.
Wanneer we er ook in slagen de astronomische eenheid te calibreren (dit gebeurt essentieel met driehoeksmeetkundige technieken), kunnen we ook de absolute afmetingen van het zonnestelsel vaststellen. De astronomische eenheid bedraagt afgerond 150 miljoen km.
Tenslotte is het dan ook mogelijk de massa van de zon te bepalen.
Baanelementen
In deze paragraaf geven we aan op welke wijze de baan van een hemellichaam in het zonnestelsel kan worden vastgelegd. Dit gebeurt aan de hand van zes parameters die de baanelementen worden genoemd.
Uit de baanelementen kan de positie van een object op een willekeurig tijdstip berekend worden.

Perihelium en aphelium
Van zodra een planeetbaan niet cirkelvormig is, is er een bepaald punt op de baan waarop de planeet zich het dichtst bij de zon bevindt. Dit punt wordt het perihelium genoemd.
Bij ellipsvormige banen is er eveneens een punt te vinden waarop de afstand tot de zon maximaal is. Dit is het aphelium.
De punten van perihelium en aphelium worden de apsiden van de planeetbaan genoemd. De lijn die beiden verbindt (en bovendien door de zon gaat), wordt daarom de apsidenlijn genoemd.
Ook voor een object dat om de aarde draait, kunnen we bovenvermelde punten aanduiden. Het dichtste punt wordt dan perigeum genoemd, het verste apogeum.
Om te beginnen willen we het baanvlak van het hemellichaam vastleggen.
- De snijlijn tussen het baanvlak van het hemellichaam en het eclipticavlak noemen we de knopenlijn. De zon ligt uiteraard op de knopenlijn, alsook de snijpunten van de baan van het hemellichaam met het eclipticavlak. Deze twee snijpunten heten de klimmende knoop (hierdoor passeert het hemellichaam het eclipticavlak van zuid naar noord) en de dalende knoop (hierdoor passeert het hemellichaam het eclipticavlak van noord naar zuid). De ligging van de knopenlijn in het eclipticavlak wordt volledig bepaald door de (heliocentrische ecliptische) lengte van de klimmende knoop (Ω) die alle waarden tussen 0° en 360° kan aannemen.
- Het baanvlak van het hemellichaam wordt dan volledig bepaald als ook de hoek wordt gegeven die dat baanvlak maakt met het eclipticavlak; deze hoek heet de inclinatie (i). Deze hoek kan alle waarden aannemen tussen 0° en 180°. Een inclinatie kleiner dan 90° impliceert een prograde beweging (in dezelfde zin als de aarde); een inclinatie groter dan 90° impliceert een retrograde beweging.
Vervolgens willen we de oriëntatie van de baan binnen het baanvlak aangeven.
- Hiervoor gebruiken we de grote as van de baan, die het perihelium en aphelium verbindt. De oriëntatie van deze lijn in het baanvlak wordt volledig bepaald door de hoek gemeten in het baanvlak tussen de richting van de klimmende knoop en de richting van het perihelium. Deze hoek wordt het argument van het perihelium (ω) genoemd en kan alle waarden tussen 0° en 360° aannemen.
Als volgende stap willen we de vorm en de schaal van de baan vastleggen.
- De vorm van de baan wordt gegeven door de excentriciteit (e), een onbenoemd getal. e = 0 staat voor een cirkel, een waarde tussen 0 en 1 geeft een ellips, bij e = 1 is de baan een parabool, en in het geval e > 1 beschrijft het hemellichaam een hyperbolische baan.
- Voor de schaal gebruiken we de periheliumafstand (q), uitgedrukt in astronomische eenheden (AU). Bij elliptische banen wordt de periheliumafstand (q) vaak vervangen door de halve grote as (a). Het verband tussen beide wordt gegeven door q = a (1 - e).
Tenslotte hebben we nog een parameter nodig die aangeeft wanneer het hemellichaam zich waar bevindt:
- Hiervoor wordt een tijdstip van periheliumdoorgang (t0) opgegeven.
Baanelementen zijn jammer genoeg niet helemaal constant in de tijd. Ten eerste verschuift het lentepunt traag in de loop van de tijd ten gevolge van de precessie. Hierdoor is het nodig een referentiejaartal op te geven, net zoals dit bij bijvoorbeeld equatoriale coördinaten gebeurt. Bovendien zijn alle baanelementen onderhevig aan wijzigingen ten gevolge van gravitationele effecten van de andere hemellichamen in het zonnestelsel. Het is dus steeds aangewezen baanelementen te gebruiken die ruwweg overeenkomen met het tijdstip waarvoor de berekeningen uitgevoerd worden
Invloed van andere hemellichamen in ons zonnestelsel
Wanneer we de beweging van een hemellichaam om de zon zeer nauwkeurig willen berekenen, kunnen we de invloed van de zwaartekracht van de andere hemellichamen van het zonnestelsel niet negeren! In de praktijk hoeven we alleen de planeten te beschouwen, omdat de andere hemellichamen van het zonnestelsel te klein zijn om een merkbare invloed te hebben. In de praktijk berekent men eerst de baan zonder rekening te houden met de invloed van de planeten, en corrigeert men dan het gevonden resultaat met behulp van storingsrekening. Deze storingen zullen zich ondermeer uiten in een langzame, periodieke verandering van de oriëntatie van de baan in de ruimte (planetaire precessie).
Verwante links
- Planetary Orbital Elements: Baanelementen van de planeten.
- Small-Body Orbital Elements: Baanelementen van alle gekende planetoïden.

