Coördinaten

Geografische coördinaten

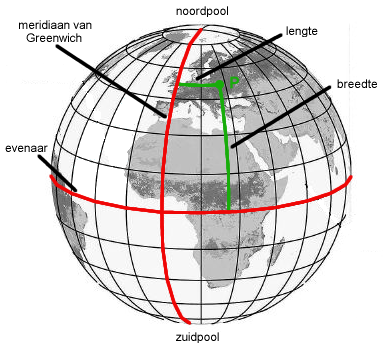Het bepalen van een plaats op aarde geschiedt met behulp van twee verschillende soorten cirkels. Eerst tekenen we de cirkels die noord- en zuidpool verbinden. Die cirkels worden middaglijnen of meridianen genoemd. Men noemt ze ook lengtecirkels. Evenwijdig aan de evenaar, kunnen we nu ook een tweede soort cirkels tekenen: de breedtecirkels. Met behulp van lengtecirkels en breedtecirkels kan je nu elke plaats op aarde bepalen.

De afstand van een punt P tot de evenaar noemen we de breedte. Aangezien de aarde bolvormig is, kunnen we die afstand als een booglengte opvatten. We drukken hem uit in graden (°). Ten noorden van de evenaar spreken we van noorderbreedte (NB), ten zuiden van zuiderbreedte (ZB). Alle plaatsen met dezelfde breedte als P liggen op de breedtecirkel door P.

Ten gevolge van een internationale overeenkomst beschouwt men de meridiaan van Greenwich als nulmeridiaan. De boog tussen de nulmeridiaan en de meridiaan of lengtecirkel waarop het punt P ligt, noemen we de lengte van dat punt. Ten oosten van Greenwich spreken we van oosterlengte (OL), ten westen van westerlengte (WL). Greenwich is de vestigingsplaats van de Koninklijke sterrenwacht van het Verenigd Koninkrijk.

Noord- en zuidpool verdelen elke lengtecirkel in twee helften. Alle plaatsen met dezelfde lengte als P liggen op de halve lengtecirkel waarop P ligt.

Elke halve lengtecirkel en elke breedtecirkel snijden elkaar in precies één punt van het aardoppervlak. Derhalve is een plaats op aarde volledig bepaald door haar lengte en breedte. De geografische coördinaten variëren van 90° NB tot 90° ZB en van 180° OL via 0° tot 180° WL. Uiteraard is -180° OL = 180° WL.

Coördinaten aan de hemel

Net zoals een plaats op het aardoppervlak met twee hoeken (lengte en breedte) wordt aangegeven, kunnen posities op de hemelbol met twee hoeken worden aangegeven.

De hemelbol en enkele belangrijke definities

Om de positie van een ster aan de hemel vast te leggen, zal de afstand waarnemer-ster geen rol spelen. Alleen de kijkrichting aan de hemel is hier van belang. Daarom kunnen we, in gedachte, alle hemelobjecten projecteren op een bol met de waarnemer als middelpunt en met oneindig grote straal. Deze denkbeeldige bol noemen we de hemelbol.

De horizon is de snijcirkel van het horizonvlak (raakvlak aan de aardbol op de plaats van de waarnemer) met deze hemelbol. De horizon verdeelt de hemelbol in een zichtbaar halfrond en een onzichtbaar halfrond. Het punt op de hemelbol vlak boven de waarnemer heet het zenit; het punt daar recht tegenover op het onzichtbare hemelhalfrond heet het nadir. Voor de overzichtelijkheid tonen de figuren verder in dit hoofdstuk alleen het zichtbare hemelhalfrond.

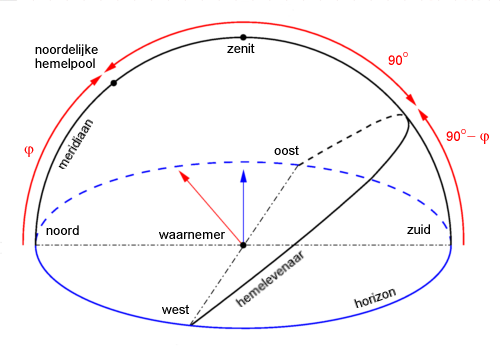
Het zichtbare snijpunt van de aardas met de hemelkoepel noemen we de noordelijke hemelpool, of kortweg de hemelnoordpool. Daar recht tegenover ligt uiteraard de hemelzuidpool. De snijcirkel van het aardse evenaarsvlak met de hemelkoepel noemen we de hemelevenaar. De hemelevenaar verdeelt de hemelkoepel op een andere manier in tweeën, namelijk in een noordelijk en een zuidelijk hemelhalfrond.

De grote cirkel gedefinieerd door hemelnoordpool en zenit noemen we de meridiaan. De snijpunten van de meridiaan met de horizon noemen we het noorden (aan de kant van de hemelnoordpool) en het zuiden (aan de andere kant). Eens deze punten gekend, worden oost en west op de gebruikelijke manier gedefinieerd.

De hemelevenaar gaat door oost en west en staat het hoogst boven de horizon in het zuiden.

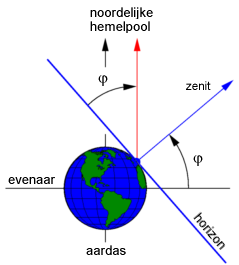
De poolshoogte is de hoogte (in hoekmaat, uiteraard) van de hemelnoordpool boven de horizon. Een eenvoudige geometrische redering op nevenstaande figuur laat zien dat die poolshoogte gelijk is aan de geografische breedte φ. Bijgevolg is de hoogte van de hemelevenaar boven het zuiden 90°-φ. Het verband tussen poolshoogte en geografische breedte is uiteraard handig voor plaatsbepaling. De hemelnoordpool kan gemakkelijk bij benadering worden teruggevonden omdat een middelmatige heldere ster, de Poolster, hier -toevallig- vlakbij staat.

Een dergelijk coördinatenstelsel vergt een referentiecirkel (voor het aardoppervlak is dat de evenaar) en een referentiepunt (voor het aardoppervlak is dat het snijpunt van de evenaar met de meridiaan van Greenwich). Eén coördinaat is dan de hoogte van het vast te leggen punt ten noorden of ten zuiden van de referentiecirkel (voor het aardoppervlak is die coördinaat de geografische breedte). De andere coördinaat is dan hoek tussen de projectie van het vast te leggen punt op de referentiecirkel en het referentiepunt (voor het aardoppervlak is die coördinaat de geografische lengte). Bovendien moet een meetrichting worden afgesproken (voor het aardoppervlak is dat oosterlengte en westerlengte).

In de sterrenkunde worden verschillende coördinatenstelsels gebruikt, afhankelijk van de toepassing die men voor ogen heeft. We overlopen nu de belangrijkste van deze coördinatenstelsels: horizoncoördinaten, equatorcoördinaten, ecliptische coördinaten en galactische coördinaten.

Horizoncoördinaten

Voor horizoncoördinaten is de referentiecirkel de horizon, het referentiepunt het zuiden en de meetrichting op de horizon mét de schijnbare dagelijkse beweging mee. De coördinaten heten hoogte h en azimut A. Azimut kan worden aangezien als een continue schaal om een richting aan te geven. Zuid correspondeert met 0°, west met 90°, noord met 180° en oost met 270°. Soms neemt men als nulpunt voor het azimut ook het noorden, en dan is oost 90°, zuid 180° en west 270°; daarom is het belangrijk steeds het nulpunt voor het azimut aan te geven.

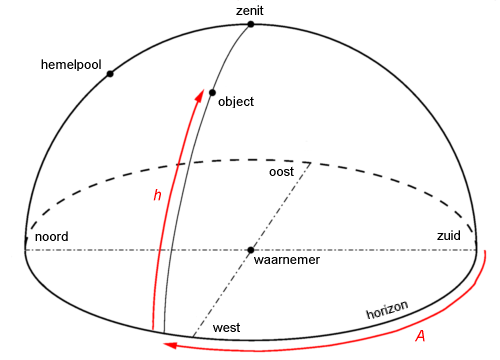
Horizoncoördinaten: hoogte h en azimut A.

Hoogte en azimut hebben het voordeel dat zij gemakkelijk kunnen worden gemeten, en, omgekeerd, gemakkelijk kunnen worden gebruikt om een object aan de hemelkoepel te lokaliseren. Gedurende de schijnbare dagelijkse beweging, veranderen deze coördinaten echter voortdurend. Ze zijn bovendien ook plaatsafhankelijk. Horizoncoördinaten zijn dus waardeloos voor bijvoorbeeld het catalogeren van sterren.

Equatorcoördinaten

We vervangen nu de horizon als referentiecirkel door de hemelevenaar en nemen als referentiepunt het zuidpunt op de hemelevenaar (d.w.z. het snijpunt van de meridiaan met de hemelevenaar). De "hoogte" t.o.v. de hemelevenaar noemen we declinatie δ; het equivalent van het azimuth is de uurhoek H, die eveneens met de dagelijkse beweging mee wordt gemeten. De uurhoek wordt doorgaans in uren gemeten in plaats van in graden. Aangezien 24h overeenstemt met 360°, correspondeert een uurhoekverschil van 1h met 15°.

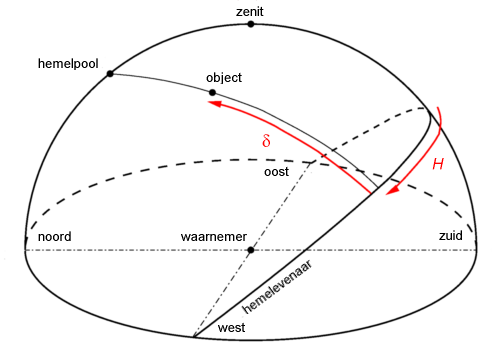
Uurcoördinaten: declinatie δ en uurhoek H.

Declinatie is niet langer tijds- en plaatsafhankelijk (voor wat betreft de dagelijkse beweging), uurhoek daarentegen wel.

Omdat de uurhoek verandert met de tijd, doen we er beter aan het lentepunt als referentie te nemen in plaats van het zuiden, omdat dit met de hemelbol meedoet aan de dagelijkse beweging. De nieuwe coördinaat heet de rechte klimming α. Deze wordt tegen de dagelijkse beweging in gemeten. Evenals de uurhoek, wordt rechte klimming doorgaans in uren gemeten in plaats van in graden. Voor de andere coördinaat gebruiken we nog steeds de declinatie δ.

Equatorcoördinaten: declinatie δ en rechte klimming α.

Omdat equatoriale coördinaten tijds- en plaatsonafhankelijk zijn, en vast verbonden zijn aan de hemelsfeer (op de precessie na), worden rechte klimming en declinatie gebruikt om in een catalogus sterposities aan te geven.

Bepalen van rechte klimming en declinatie

Om nauwkeurig de rechte klimming en declinatie van een hemellichaam te meten, kan een meridiaankijker gebruikt worden. Zulk een kijker is perfect in lijn met de noord-zuid as, en kan dus enkel objecten bekijken die pal op de meridiaan staan. Met een meridiaankijker kan een waarnemer het tijdstip bepalen waarop een ster door de zuidelijke meridiaan trekt, alsook op welke hoogte dit gebeurt.

De sterrentijd op het moment dat de ster door het zuiden passeert, is exact gelijk aan de rechte klimming van de ster. De sterrentijd is immers het verschil in rechte klimming tussen de meridiaan en het lentepunt, welk het referentiepunt is voor de equatoriale coördinaten.

Uit de hoogte h van de ster wanneer ze door het zuiden trekt, kan rechtstreeks de declinatie δ gehaald worden, gezien δ = h + φ - 90°, met φ de breedteligging van de waarnemingsplaats.

Ecliptische coördinaten

Ecliptische coördinaten zijn volledig analoog aan de hierboven beschreven equatorcoördinaten, maar met de hemelevenaar vervangen door de ecliptica. Het referentiepunt is nog steeds het lentepunt, dat immers ook op de ecliptica ligt. De coördinaat corresponderend met declinatie heet ecliptische breedte β en de coördinaat corresponderend met rechte klimming heet ecliptische lengte λ. De ecliptische lengte wordt, net zoals de rechte klimming, tegen de schijnbare dagelijkse beweging in gemeten, dat is mét de schijnbare jaarlijkse beweging van de zon mee. In de loop van het jaar neemt de ecliptische lengte van de zon dus steeds toe.

Ecliptische coördinaten worden vooral gebruikt in de context van het zonnestelsel. De meeste planeten en hemellichamen in ons zonnestelsel beschrijven een baan in een vlak dat dicht bij het eclipticavlak ligt.

Galactische coördinaten

Galactische lengte en breedte zijn analoog aan ecliptische lengte en breedte. De referentiecirkel is nu de galactische equator (de snijcirkel van het symmetrievlak van ons Melkwegstelsel) en het referentiepunt is de richting van het centrum van ons Melkwegstelsel. Hierdoor loopt de galactische equator aan de hemel door de melkweg. De positie van de galactische equator wordt volledig bepaald door de positie van de ermee corresponderende galactische noordpool, en die is (J2000) α=12h52m en δ=+27°08'. Het centrum van ons Melkwegstelsel ligt in het sterrenbeeld Boogschutter op α=17h45m en δ=-28°56'.

Galactische coördinaten worden vooral gebruikt voor de studie van ons Melkwegstelsel en van sterrenstelsels in het algemeen.

Verwante links